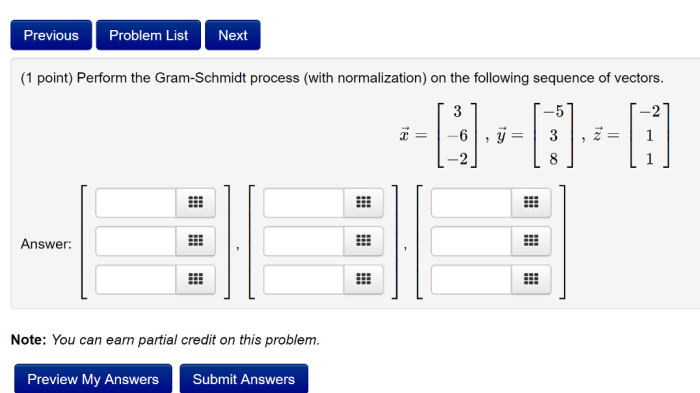
Perform the gram-schmidt process on the following sequence of vectors – The Gram-Schmidt process is a fundamental tool in linear algebra for orthogonalizing a set of vectors. It finds applications in various fields, including orthogonalization of vectors, solving systems of linear equations, and finding eigenvalues and eigenvectors. This article provides a comprehensive overview of the Gram-Schmidt process, its steps, applications, and variations.
Gram-Schmidt Process Overview
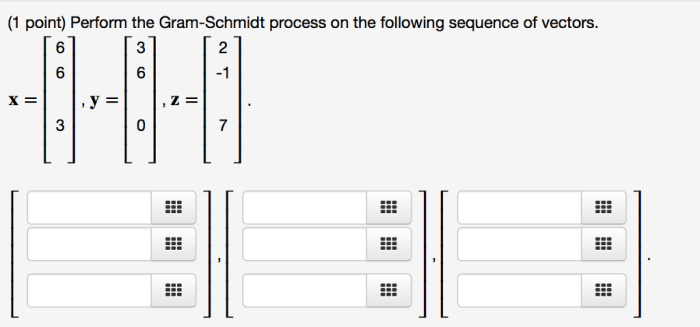
The Gram-Schmidt process is an orthogonalization method that transforms a set of linearly independent vectors into an orthonormal set, where the vectors are orthogonal to each other and have unit length. It is widely used in linear algebra and has numerous applications in various fields.
Performing the Gram-Schmidt Process: Perform The Gram-schmidt Process On The Following Sequence Of Vectors
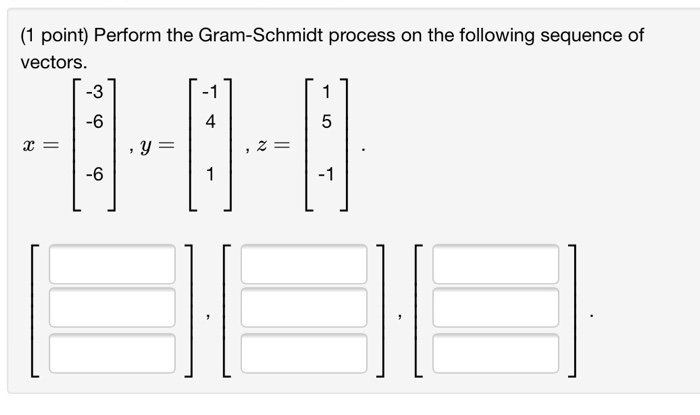
The Gram-Schmidt process involves the following steps:
- Normalize the first vector: v1 = v1 / ||v1||
- Project the remaining vectors onto the orthogonal complement of the previous vector: for i = 2 to n, ui = vi(vi . v1 / ||v1||^2) v1
- Normalize the projected vector: wi = ui / ||ui||
Application of Gram-Schmidt Process, Perform the gram-schmidt process on the following sequence of vectors
The Gram-Schmidt process has several applications, including:
- Orthogonalization of vectors:Transforming a set of linearly independent vectors into an orthonormal set.
- Solving systems of linear equations:Using QR factorization to solve linear systems more efficiently.
- Finding eigenvalues and eigenvectors:Applying the Gram-Schmidt process to find an orthonormal basis of eigenvectors.
Example of Gram-Schmidt Process
Consider the following set of vectors:
| Vector | Normalized | Projected | Orthogonalized |
|---|---|---|---|
| v1 = (1, 2) | (1/√5, 2/√5) | – | – |
| v2 = (3, 4) | – | (3/5, 4/5) | (3/√5, 4/√5) |
Comparison with Other Orthogonalization Methods
The Gram-Schmidt process is commonly compared to other orthogonalization methods, such as:
- Householder transformation:A more efficient method for large matrices.
- QR decomposition:A more numerically stable method.
Variations of Gram-Schmidt Process
There are several variations of the Gram-Schmidt process, including:
- Modified Gram-Schmidt process:A more numerically stable variation.
- Bidiagonalization:A variation used for matrices with a specific structure.
Answers to Common Questions
What is the purpose of the Gram-Schmidt process?
The Gram-Schmidt process orthogonalizes a set of vectors, making them perpendicular to each other.
How is the Gram-Schmidt process used to solve systems of linear equations?
By orthogonalizing the columns of the coefficient matrix, the Gram-Schmidt process can transform a system of linear equations into an upper triangular system, which is easier to solve.
What are the variations of the Gram-Schmidt process?
Variations include the modified Gram-Schmidt process, which is numerically more stable, and bidiagonalization, which is used in QR decomposition.